Question

Bill is playing a game of chance with the following payout. 30% of the time you will lose 20 dollars, 20% of the time you will lose 40 dollars. 10% of the time you will win 50 dollars, 40% of the time you will win 5 dollars. Find the expected value of the event and explain if Bill should play this game based on the mathematical expectation.

please helpppop asappppp and show work so I understand please ​


Anybody know this??? please help

Answer 1

The expected value of playing the game is -$7.

Bill should not play this game.

Explanation:

The probability distribution of gain and loss is as follows:

X P (X)

-$20 0.30

-$40 0.20

$50 0.10

$5 0.40

Total 1.00

The expected value of a probability distribution is given by:

`E(X)=\sum {X* P(X)}`

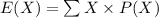
Compute the expected value of playing the game of chance as follows:

`E(X)=\sum {X* P(X)}`

`=(-\$20* 0.30)+(-\$40* 0.20)+(\$50* 0.10)+($5* 0.40)\\\\=-\$6-\$8+\$5+\$2\\\\=-\$7`

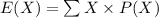
The expected value of playing the game is -$7.

The expected value of the game suggests that Bill will incur a loss of $7 if he plays.

So, it is safe not to play the game.