Question

A manufacturer of banana chips would like to know whether its bag filling machine works correctly at the 430 gram setting. It is believed that the machine is underfilling or overfilling the bags. A 23 bag sample had a mean of 435 grams with a variance of 841. Assume the population is normally distributed. A level of significance of 0.05 will be used. Specify the type of hypothesis test.

Answer 1

`t=(435-430)/((29)/(√(23)))=0.827`

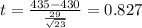
The degrees of freedom are given by:

`df=n-1=23-1=22`

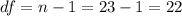
And the p value taking in count that we have a bilateral test we got:

`p_v =2*P(t_((22))>0.827)=0.417`

Since the p value is higher than the significance level of 0.05 we have enough evidence to conclude that the true mean is not significantly different from 430 the required value

Explanation:

Information given

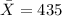`\bar X=435` represent the mean for the weight

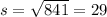`s=√(841)=29` represent the sample standard deviation

`n=23` sample size

`\mu_o =430` represent the value that we want to verify

`\alpha=0.05` represent the significance level

t would represent the statistic

`p_v` represent the p value

System of hypothesis

We are trying to proof if the filling machine works correctly at the 430 gram setting, so then the system of hypothesis for this case are:

Null hypothesis:
`\mu = 430`

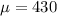
Alternative hypothesis:
`\mu \\eq 430`

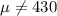
In order to cehck the hypothesis the statistic for a one sample mean test is given by

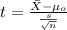`t=(\bar X-\mu_o)/((s)/(√(n)))` (1)

Replacing the info given we have this:

`t=(435-430)/((29)/(√(23)))=0.827`

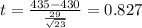
The degrees of freedom are given by:

`df=n-1=23-1=22`

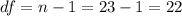
And the p value taking in count that we have a bilateral test we got:

`p_v =2*P(t_((22))>0.827)=0.417`

Since the p value is higher than the significance level of 0.05 we have enough evidence to conclude that the true mean is not significantly different from 430 the required value