Question

g According to the U.S. Census Bureau, 11% of children in the United States lived with at least one grandparent in 2009 (USA TODAY, June 30, 2011). Suppose that in a recent sample of 1630 children, 228 were found to be living with at least one grandparent. At a 5% significance level, can you conclude that the proportion of all children in the United States who currently live with at least one grandparent is higher than 11%? Use both the p-value and the critical-value approaches.

Answer 1

`z=\frac{0.14 -0.11}{\sqrt{(0.11(1-0.11))/(1630)}}=3.871`

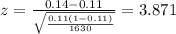
Critical approach

`z_(crit)= 1.64`

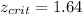
Since the calculated value is higher than the critical value we have enough evidence to conclude that the true proportion is significantly higher than 0.11 or 11%

P value

We are conducting a right tailed test so then the p value is given by:

`p_v =P(z>3.871)=0.000054`

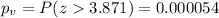
And we see that is a very low value compared to the significance level of 0.05 so then we have enough evidence to conclude that the true proportion is significantly higher than 0.11.

Explanation:

Information provided

n=1630 represent the random sample selected

X=228 represent the children were found to be living with at least one grandparent

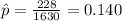`\hat p=(228)/(1630)=0.140` estimated proportion of children were found to be living with at least one grandparent

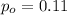`p_o=0.11` is the value to verify

`\alpha=0.05` represent the significance level

z would represent the statistic

`p_v` represent the p value

System of hypothesis

We want to verify if the % of children who live with at least one grandparent is higher than 11%, so then the system of hypothesis is .:

Null hypothesis:
`p\leq 0.11`

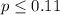
Alternative hypothesis:
`p >0.11`

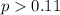
The statistic for this case is given by:

`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

Replacing the info given we got:

`z=\frac{0.14 -0.11}{\sqrt{(0.11(1-0.11))/(1630)}}=3.871`

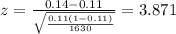
Critical approach

we need to find a critical value in the normal standard distribution who accumulate 0.05 of the area in the left and for this case this value is:

`z_(crit)= 1.64`

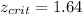
Since the calculated value is higher than the critical value we have enough evidence to conclude that the true proportion is significantly higher than 0.11 or 11%

P value

We are conducting a right tailed test so then the p value is given by:

`p_v =P(z>3.871)=0.000054`

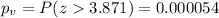
And we see that is a very low value compared to the significance level of 0.05 so then we have enough evidence to conclude that the true proportion is significantly higher than 0.11.