Question

The score distribution shown in the table is for all students who took a yearly AP statistics exam. An AP statistics teacher had 6565 students preparing to take the AP exam. Though they were obviously not a random​ sample, he considered his students to be​ "typical" of all the national students.​ What's the probability that his students will achieve an average score of at least​ 3?

Answer 1

Explanation:

The question is incomplete because the data is missing, i.e. the probability that you will score 5, 4, 3, 2, 1.

But it is resolved as follows:

`P(x\geq 3) = P((x - m)/((sd)/(√(n) ) ) \geq (3 - m)/((sd)/(√(n) )))\\\\`

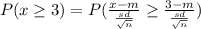
where m is the mean and sd is the standard deviation.

the m is calculated by the sum of the multiplication of the score by the probability of this

that is to say,

score probability

5 0.2

4 0.3

3 0.1

2 0.3

1 0.1

m = 5*0.2 + 4*0.3 + 3*0.1 + 2*0.3 + 1*0.1

m = 3.2

However, the standard deviation will be calculated by

sd =
`√(\\)`∑
`(x - m)^(2)*p`

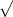that is, knowing the mean already, we can calculate the standard deviation, following the example:

sd =
`√([(5-3.2)^2] *0.2 + [(4-3.2)^2] *0.3 + [(3-3.2)^2] *0.1 + [(2-3.2)^2] *0.3 + [(1-3.2)^2] *0.1 )`

sd =
`√(1.76)`

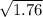
sd = 1.327

And also n = 5, because it's 5 scores. We replace in the initial equation:

`P(x\geq 3) = P(Z \geq (3 - 3.2)/((1.327)/(√(5) )))\\\\`

`P(x\geq 3) = P(Z \geq -0.337)\\\\\\`

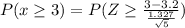
Therefore for the example the number z is -0.337, which if in the normal distribution table corresponds to 0.3520, that is the probability that the average is at least 3, for the example is 35.20 %.