Answer: 43.5g of carbon dioxide it produce at 95% efficiency
Step-by-step explanation:
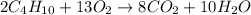
To calculate the moles, we use the equation:
moles of butane =
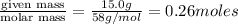
According to stoichiometry:
2 moles of butane gives = 8 moles of carbon dioxide
Thus 0.26 moles of butane gives=
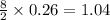 moles of carbon dioxide
moles of carbon dioxide
Mass of
 produced=
produced=

As yield of the reaction is 95%, the amount of
 produced =
produced =
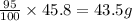
Thus 43.5g of carbon dioxide it produce at 95% efficiency