Question

This table gives the value of an investment for the first 14 years after the initial investment was made. The data can be modeled using an exponential function.

Years 2 4 6 8 10 12 14
Investment value $692 $952 $1,304 $1,813 $2,316 $3,256 $4,718
Based on the data, which amount is closest to the value of the investment 18 years after the initial investment? PLS HURRY I NEED THIS ANSWERED NOW, WILL GIVE 95 POINTS

Answer 1

General form of an exponential equation:
`y=ab^x`

where:

• a is the initial value
• b is the growth factor
• x is the independent variable
• y is the dependent variable

Let x = years

Let y = investment value

Use (2, 692) and (4, 952) to find a and b of the exponential equation:

`ab^2=692`

`ab^4=952`

`\implies (ab^4)/(ab^2)=(952)/(692)`

`\implies b^2=(238)/(173)`

`\implies b=\sqrt{(238)/(173)}=1.17\:\textsf{(nearest hundredth)}`

`\implies ab^2=a\left((238)/(173)\right)=692`

`\implies a=\left((59858)/(119)\right)=503.01\:\textsf{(nearest hundredth)}`

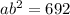
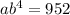
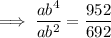
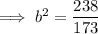
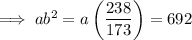
Therefore, the exponential equation is:

`y=503.01(1.17)^x`

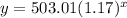
18 years after the initial investment is when
`x=18`:

`\implies 503.01(1.17)^(18)=8490`

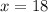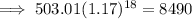
Therefore, the amount closest to the value of the investment 18 years after the initial investment is $8490

(If you use the exact values for a and b rather than the rounded values, the amount is $8879)