Question

PLZZZZ HELP!!!

Bill is playing a game of chance with the following payout. 30% of the time you will lose 20 dollars, 20% of the time you lose 40 dollars, 10% of the time you win 50 dollars, 40% of the time you win 5 dollars. Find the expected value of the event and explain if Bill should play this game based on the mathematical expectation.

Answer 1

• Expected Value= -$7
• Bill should not play the game

Explanation:

In the game, these are the payout:

• 30% of the time you will lose 20 dollars.
• 20% of the time you lose 40 dollars.
• 10% of the time you win 50 dollars
• 40% of the time you win 5 dollars.

To compute the expected value, take note that a loss is negative while a win is positive.

`E(X)=\sum_(i=1)x_1P(x_1)`

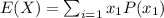
Therefore:

E(X)=(-20*0.3)+(-40*0.2)+(50*0.1)+(5*0.4)

E(X)=-7

• The expected value of the event is -$7.
• Based on the negative expectation, Bill should not play this game as he is expected to incur a loss.