Question

A 100-foot rope from the top of a tree house to the ground forms a 45∘ angle of elevation from the ground. How high is the top of the tree house? Round your answer to the nearest tenth of a foot.

Answer 1

The height of tree house is 70.71 feet

Explanation:

We are given that A 100-foot rope from the top of a tree house to the ground forms a 45∘ angle of elevation from the ground

Refer the attached figure

Length of rope AC = Hypotenuse =100 feet

The top of a tree house to the ground forms a 45∘ angle of elevation from the ground =
`\angle ACB = 45^(\circ)`

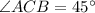
We are supposed to find the height of tree house i.e.AB = Perpendicular

So, Using trigonometric ratio

`Sin \theta = (perpendicular)/(Hypotenuse)\\Sin 45= (AB)/(AC)\\(1)/(√(2))=(AB)/(100)\\100 * (1)/(√(2))=AB\\70.71=AB`

Hence The height of tree house is 70.71 feet