That's the Riemann Zeta function. Here s is a complex number. If you can prove that all the non-trivial zeros of ζ(s) (which includes its analytic continuation to the entire complex plane) are on the line Re(s) = -1/2 then you will become a famous mathematician. You didn't even ask a question; not a very auspicious start, but don't give up.
If we restrict s to the reals, as Euler first did, we can prove there are an infinity of primes. Ever since the Zeta function has been closely related to the prime numbers.
One fun fact is ζ(-1) = -1/12, which has spawned lots of bad math claiming the sum of the natural numbers is -1/12,
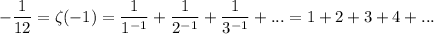
Here it is in Ramanujan's first letter to Hardy.