Answer:
speed after one riveting operation = 230.5 rpm
mass moment of inertia = 9.90 kg
Step-by-step explanation:
given data
torque energy = 2.5 kW = 2500 W
mass = 125 kg
radius = 700 mm
energy = 1000 J
Speed of the flywheel N = 240 rpm
solution
we know here Speed of the flywheel N so here angular speed ω
ω =
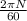 .....................1
.....................1
ω =
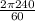
ω = 25.13 rad/s
so here
change in energy is
ΔE = E1 - E2 ..............2
ΔE = 2500 - 1000
ΔE = 1500 J/sec
and
I = mr² .........3
I = 125 × 0.7²
I = 61.25 kg-m²
and ΔE is express as here
ΔE = 0.5 × I × (ω² - ω1² ) ........4
put here value and we get
1500 = 0.5 × 61.25 × (25.13² - ω1² )
ω1 = 24.13 rad /s
and
reduction in speed after one riveting operation will be
N =
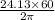
speed after one riveting operation = 230.5 rpm
and
for 35 rpm
ω1 =
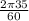
ω1 = 3.65
so ΔE will be here
ΔE = 0.5 × mr² × (ω² - ω1² ) ....................5
put here value and we get m
1500 = 0.5 × m (0.7)² × (25.13² - 3.65² )
solve it we get
mass moment of inertia = 9.90 kg