Answer:
Step-by-step explanation:
Mirror formation in mirror A
focal length f = - 10 cm ( concave mirror )
Let u be object distance , v is image distance .
In case image is virtual
v / u = 2
v = 2u
Mirror formula
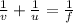
Putting the values
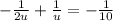
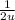 =
=
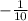
u = -5 cm
In case image is real
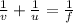
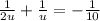
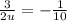
u =
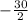
u = - 15 cm