Question

Linda shoots an arrow at a target in an archery competition. The arc of the arrow can be modeled by the equation y = −0.02x2 + 0.65x + 4, where x is the horizontal distance (in meters) from Linda and y is the height (in meters) of the arrow. How far from Linda does the arrow hit the ground? Round to the nearest tenth.

Answer 1

Linda was 37.8 m away when the arrow hit the ground

Explanation:

We are given that The arc of the arrow can be modeled by the equation :

`y = -0.02x^2 + 0.65x + 4`

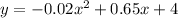
Where x is the horizontal distance (in meters) from Linda

y is the height (in meters) of the arrow.

Now we are supposed to find How far from Linda does the arrow hit the ground

So, y must be 0 when the arrow hits the ground

So, Substitute y = 0 in the equation :

`y = -0.02x^2 + 0.65x + 4\\0 = -0.02x^2 + 0.65x + 4\\0.02x^2-0.65x-4=0\\0.02(x-37.79)(x+5.29)=0\\x=37.79,-5.29`

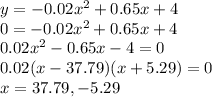
Since distance cannot be negative

So,Linda was 37.8 m away when the arrow hit the ground