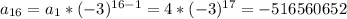Answer:
r = -3
16th term: -516560652
Explanation:
Let's use the formula for a geometric sequence:
 , where
, where
 is the nth term,
is the nth term,
 is the first term, and r is the common ratio
is the first term, and r is the common ratio
Here, we know the first term is 4. To find r, let's plug in 8 for n and -8748 for
 :
:

-8748 = 4 *

-8748 = 4 *
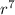
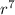 = -2187
= -2187
r = -3
So we know that the common ratio is -3. Now, we want to find the 16th term, so n = 16: