Question

Suppose $1750 is put into an account that pays an annual rate of 4.5%

compounded quarterly. How much will be in the account after 6 years?(round to the
hundredth place)

Answer 1

There will be $2288.98 in the account after 6 years

Explanation:

We are given that $1750 is put into an account that pays an annual rate of 4.5% compounded quarterly.

So, Principal = $1750

Rate of interest = 4.5%

No. of compounds per year = 4

Time = 6 years

Formula :
`A =P(1+(r)/(n))^(nt)`

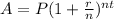
Where A = Amount

P = Principal

r = rate of interest

n = no. of compounds per year

t = time

Substitute the values in the formula :

`A =1750(1+(4.5)/(400))^(4 * 6)`

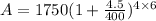
A=2288.98

Hence There will be $2288.98 in the account after 6 years