Answer:
A; x + 1
Explanation:
Since the viniculum in a fraction represents division, we can rewrite the expression like this:
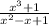
We can already see that
 could be factored:
could be factored:
Since anything with a "one" as its base will remain one, we can rewrite:
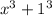
Now, we can apply the "sum of cubes" formula:
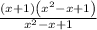
Cancelling out!
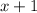
Thusly, you are correct and the remainder is
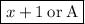 .
.
Hope this helps! ((: