Question

Let X represent the number of occupants in a randomly chosen car on a certain stretch of highway during morning commute hours. A survey of cars showed that the probability distribution of X is as follows. x 1 2 3 4 5 P(x) 0.70 0.15 0.10 0.02 (a) Find P(4). (b) Find the probability that a car has at least 3 occupants. (c) Find the probability that a car has fewer than 3 occupants. (d) Compute the mean µX. (e) Compute the standard deviation σX.

Answer 1

a) P(4)=0.03

b) P(x≥3)=0.15

c) P(x<3)=0.85

d) µX=1.52

e) σX=1.69

Explanation:

The question is incomplete:

The variable X has the following probability distribution:

x 1 2 3 4 5

P(x) 0.7 0.15 0.10 0.03 0.02

a) The probability P(x=4) can be read from the table

`P(4)=0.03`

b) The probability that there are at least 3 occupants in the car is P(x≥3).

`P(x\geq3)=P(3)+P(4)+P(5)\\\\P(x\geq3)=0.10+0.03+0.02\\\\P(x\geq3)=0.15`

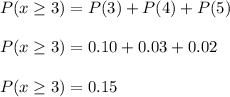
c) The probability that a car has fewer than 3 occupants (P(x<3)) is:

`P(x<3)=1-P(x\geq3)=1-0.15=0.85`

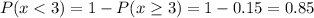
d) The mean can be calculated as:

`\mu_x=\sum_(i=1)^5p_i\cdot x_i\\\\\mu_x=0.7*1+0.15*2+0.10*3+0.03*4+0.02*5\\\\\mu_x=0.7+0.30+0.30+0.12+0.10\\\\ \mu_x=1.52`

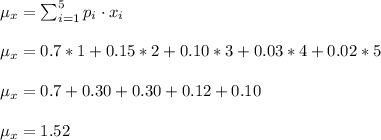
e) The standard deviation can be calculated as:

`\sigma_x=\sqrt{\sum_(i=1)^5p_i(x_i-\mu_x)^2}}\\\\ \sigma_x=√(0.7(1-1.52)^2+ 0.15(2-1.52)^2+ 0.1(3-1.52)^2+ 0.03(4-1.52)^2 +0.02(5-1.52)^2)\\\\ \sigma_x=√(0.7*0.2704+0.15*0.2304+0.1*2.1904+0.03*6.1504+0.03*12.1104)\\\\\sigma_x=√(0.18928+0.06912+0.65712+0.738048+1.21104)\\\\ \sigma_x=√(2.8646)\\\\ \sigma_x=1.69`