We have been given that Marissa's Beauty Salon has six hair dryers that each require 500 watts when switched on.We are asked to find the cost to run all six dryers for 7 hours, at a cost of $0.15 per kWh.
First of all, we will find watts of energy used to switch on 6 hair dryers.
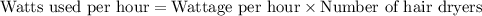
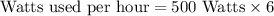
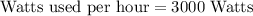
Now we will convert watts into kilowatts. We know that 1 kW is equal to 1000 W.
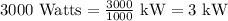
So 3 kW are used for 7 dryers for 1 hour. Now we will multiply 3 kW by 7 to find kWs used in 7 hours as:
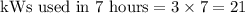
Since the cost of 1 kWh is $0.15, so to find cost for 21 kW/h, we will multiply $0.15 by 21.
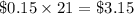
Therefore, it will cost $3.15 to run all six dryers for 7 hours.