Question

Mary lives on a corner lot. The neighborhood children have been cutting diagonally across her lawn instead of walking around the yard. If the diagonal distance across the lawn is 50 ft and the longer part of the sidewalk is twice the shorter length, how many feet are the children saving by cutting the lawn? round to the nearest foot if necessary.

Answer 1

17 feet

Explanation:

Length of the diagonal=50 feet

Let the shorter part of the sidewalk =x

Since the longer part of the sidewalk is twice the shorter length,

Length of the longer part of the sidewalk =2x

First, we determine the value of x.

Using Pythagoras Theorem and noting that the diagonal is the hypotenuse.

`50^2=(2x)^2+x^2\\5x^2=2500\\$Divide both sides by 5\\x^2=500\\x=√(500)=10√(5) \:ft`

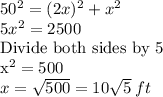
The length of the shorter side =
`10√(5) \:ft`

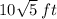
The length of the longer side =
`20√(5) \:ft`

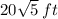
Total Distance =
`10√(5)+ 20√(5)=67 \:feet`

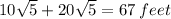
Difference in Distance

67-50=17 feet

The children are saving 17 feet by cutting the lawn diagonally.