Answer:
17 feet
Explanation:
Length of the diagonal=50 feet
Let the shorter part of the sidewalk =x
Since the longer part of the sidewalk is twice the shorter length,
Length of the longer part of the sidewalk =2x
First, we determine the value of x.
Using Pythagoras Theorem and noting that the diagonal is the hypotenuse.
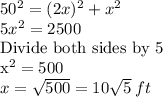
The length of the shorter side =

The length of the longer side =
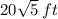
Total Distance =
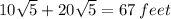
Difference in Distance
67-50=17 feet
The children are saving 17 feet by cutting the lawn diagonally.