Question

Water vapor at 100 psi, 500 F and a velocity of 100 ft./sec enters a nozzle operating at steady sate and expands adiabatically to the exit, where the pressure is 40 psia. If the isentropic nozzle efficiency is 95%, determine for the nozzle,

(a) the exit velocity of the steam in ft./sec, and

(b) the amount of entropy produced in BTU/ lbm R.

Answer 1

a)exit velocity of the steam, V2 = 2016.8 ft/s

b) the amount of entropy produced is 0.006 Btu/Ibm.R

Step-by-step explanation:

Given:

P1 = 100 psi

V1 = 100 ft./sec

T1 = 500f

P2 = 40 psi

n = 95% = 0.95

a) for nozzle:

Let's apply steady gas equation.

`h_1 + ((v_1) ^2)/(2) = h_2 + ((v_2)^2)/(2)`

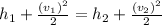
h1 and h2 = inlet and exit enthalpy respectively.

At T1 = 500f and P1 = 100 psi,

h1 = 1278.8 Btu/Ibm

s1 = 1.708 Btu/Ibm.R

At P2 = 40psi and s1 = 1.708 Btu/Ibm.R

1193.5 Btu/Ibm

Let's find the actual h2 using the formula :

`n = (h_1 - h_2*)/(h_1 - h_2)`

`n = (1278.8 - h_2*)/(1278.8 - 1193.5)`

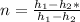
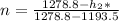
solving for h2, we have

`h_2 = 1197.77 Btu/Ibm`

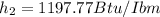
Take Btu/Ibm = 25037 ft²/s²

Using the first equation, exit velocity of the steam =

`(1278.8 * 25037) + ((100)^2)/(2)= (1197.77*25037)+ ((V_2)^2)/(2)`

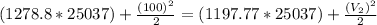
Solving for V2, we have

V2 = 2016.8 ft/s

b) The amount of entropy produced in BTU/ lbm R will be calculated using :

Δs = s2 - s1

Where s1 = 1.708 Btu/Ibm.R

At h2 = 1197.77 Btu/Ibm and P2 =40 psi,

S2 = 1.714 Btu/Ibm.R

Therefore, amount of entropy produced will be:

Δs = 1.714Btu/Ibm.R - 1.708Btu/Ibm.R

= 0.006 Btu/Ibm.R