Question

A machine that fills beverage cans is supposed to put 12 ounces of beverage in each can. The standard deviation of the amount in each can is 0.12 ounce. The machine is overhauled with new components, and ten cans are filled to determine whether the standard deviation has changed. Assume the fill amounts to be a random sample from a normal population.

Perform a hypothesis test to determine whether the standard deviation differs from 0.12 ounce. Use the level of significance.

Answer 1

`\chi^2 =(10-1)/(0.0144) 0.0217 =13.54`

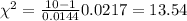
The degrees of freedom are:

`df=n-1=10-1=9`

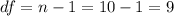
Now we can calculate the p value using the alternative hypothesis:

`p_v =2*P(\chi^2 >13.54)=0.279`

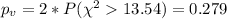
Since the p value is higher than the signficance level assumed of 0.05 we have enough evidence to FAIL to reject the null hypothesis and there is no evidence to conclude that the true deviation differs from 0.12 ounces

Explanation:

Assuming the following data:"12.14 12.05 12.27 11.89 12.06

12.14 12.05 12.38 11.92 12.14"

We can calculate the sample deviation with this formula:

`s =\sqrt{(\sum_(i=1)^n (X_i -\bar X)^2)/(n-1)}`

`n=10` represent the sample size

`\alpha=0.05` represent the confidence level

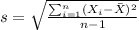
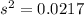`s^2 =0.0217` represent the sample variance

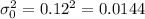`\sigma^2_0 =0.12^2= 0.0144` represent the value to verify

Null and alternative hypothesis

We want to determine whether the standard deviation differs from 0.12 ounce, so the system of hypothesis would be:

Null Hypothesis:
`\sigma^2 = 0.0144`

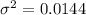
Alternative hypothesis:
`\sigma^2 \\eq 0.0144`

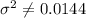
The statistic can be calculated like this;

`\chi^2 =(n-1)/(\sigma^2_0) s^2`

`\chi^2 =(10-1)/(0.0144) 0.0217 =13.54`

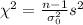
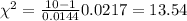
The degrees of freedom are:

`df=n-1=10-1=9`

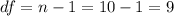
Now we can calculate the p value using the alternative hypothesis:

`p_v =2*P(\chi^2 >13.54)=0.279`

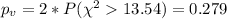
Since the p value is higher than the signficance level assumed of 0.05 we have enough evidence to FAIL to reject the null hypothesis and there is no evidence to conclude that the true deviation differs from 0.12 ounces