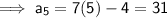Answer:
An arithmetic sequence is an ordered set of numbers where the difference between each consecutive term is the same (this is called the "common difference").
The formula for each term in an arithmetic sequence is:
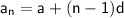
where:
- a is the first term in the sequence
- d is the common difference between consecutive terms
- n is the position of the term in the sequence
Example
Sequence: 3, 10, 17, 24, 31, ...
The first term in the sequence is 3, therefore a = 3
The common difference can be found by subtracting one term from the next: d = 10 - 3 = 7
Substituting these values into the equation for the nth term:
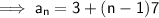
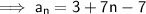
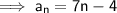
Therefore, if we want to find the 5th term of the sequence, simply input
n = 5 into the found equation: