Answer:
a) growth
b) 3%
c) 6 years (since the beginning of the decade)
Explanation:
Given:
The population P (in thousands) of Austin, Texas during a recent decade can be approximated by
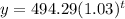 when t is the number of years since the beginning of the decade.
when t is the number of years since the beginning of the decade.
General form of an exponential function:

where:
- a is the y-intercept (or initial value)
- b is the base (or growth factor)
- x is the independent variable
- y is the dependent variable
If
 then it is an increasing function
then it is an increasing function
If
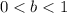 then it is a decreasing function
then it is a decreasing function
a) The model represents exponential growth as 1.03 > 1
b) The annual percent increase of the population is 3%
1.03 - 1 = 0.03
0.03 x 100 = 3%
c) To estimate when was population about 590,000 set y = 590 and solve for t:
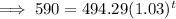

Take natural logs of both sides:
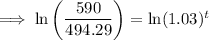
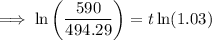
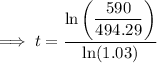
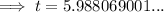
Therefore the population was about 590,000 6 years since the beginning of the decade.