Question

A catapult launches a boulder with an upward velocity of 120 ft/s. The height of the boulder, h,

in feet after t seconds is given by the function h=-167 + 120t + 10. How long does it take to
reach maximum height? What is the boulder's maximum height? Round to the nearest
hundredth, if necessary.
a. Reaches a maximum height of 235.00 feet in 3.75 seconds.
b. Reaches a maximum height of 10.00 feet in 7.50 seconds.
c. Reaches a maximum height of 7.58 feet in 3.75 seconds.
d. Reaches a maximum height of 15.16 feet in 7.5 seconds.

Answer 1

Reaches a maximum height of 235.00 feet in 3.75 seconds.

Explanation:

The height of the boulder, h, in feet after t seconds is given by the function is given by :

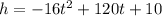`h=-16t^2+120t+10` .....(1)

For maximum height, put
`(dh)/(dt)=0`

i.e.

`(d(-16t^2+120t+10))/(dt)=0\\\\-32t+120=0\\\\32t=120\\\\t=3.75\ s`

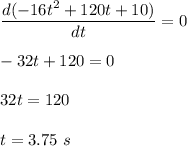
Put t = 3.75 in equation (1). So,

`h=-16(3.75)^2+120(3.75)+10\\\\h=235\ \text{feet}`

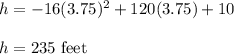
So, the boulder's maximum height is 235 feets and it takes 3.75 s to reach to its maximum height.