Question

What is the radian measure of the central angle of an arc that has an arc length of 5 units and radius of 2 units

Answer 1

Central angle = θ = 2.5 radians

Explanation:

The radian measure of central angle is given by

`\theta = (s)/(r)`

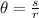
Where s is the arc length, r is the radius of circle and θ is angle in radians

We are given an arc length of 5 units

`s = 5`

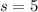
We are given radius of 2 units

`r = 2`

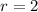
Therefore, the central angle in radians is

`\theta = (5)/(2)\\\\\theta = 2.5 \: rad`

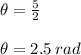
Bonus:

Radian is a unit which we use to measure angles.

1 Radian is the angle that results in an arc having a length equal to the radius.

Degree is another unit that we use to measure angles.

There are 360° in a circle.

There are 2π radians in a circle.