Question

On a coordinate plane, two parabolas open up. The solid-line parabola, labeled f of x, goes through (negative 2, 4), has a vertex at (0, 0), and goes through (2, 4). The dashed-line parabola, labeled g of x, goes through (negative 6, 10), has a vertex at (negative 4, 6), and goes through (negative 2, 10).

What is the equation of the translated function, g(x), if

f(x) = x2?


g(x) = (x – 4)2 + 6

g(x) = (x + 6)2 – 4

g(x) = (x – 6)2 – 4

g(x) = (x + 4)2 + 6

Answer 1

The answer is D just took the test.

Answer 2

`y = (x+4)^(2)+6`

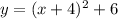
Explanation:

The parabola with vertex at point (h,k) is described by the following model:

`y - k = C\cdot (x-h)^(2)`

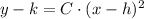
The equation which satisfies the conditions described above:

`y - 6 = (x+4)^(2)`

`y = (x+4)^(2)+6`

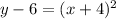
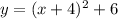
The two points are evaluated herein:

x = -6

`y =(-6+4)^(2)+6`

`y = (-2)^(2)+6`

`y = 4 + 6`

`y = 10`

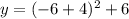
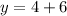
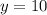
x = -2

`y = (-2+4)^(2)+6`

`y = 2^(2) + 6`

`y = 4 + 6`

`y = 10`

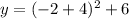
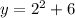
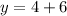
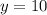
The equation of the translated function is
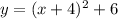`y = (x+4)^(2)+6`.