Question

Which are the solutions of the equation x^4 - 5x^2 - 36 = 0

Answer 1

x = ± 3, x = ± 2i

Explanation:

Given

`x^(4)` - 5x² - 36 = 0

Use the substitution u = x² then the equation is

u² - 5u - 36 = 0 ← in standard form

(u - 9)(u + 4) = 0 ← in factored form

Equate each factor to zero and solve for u

u - 9 = 0 ⇒ u = 9

u + 4 = 0 ⇒ u = - 4

This indicates there will be 2 real roots and 2 complex roots

Change back to find values of x, that is

u = 9 ⇒ x² = 9 ⇒ x = ±
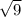`√(9)` = ± 3 ← real roots

u = - 4 ⇒ x² = - 4 ⇒ x = ±
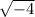`√(-4)` = ± 2i ← imaginary roots

Answer 2

4x-10x = 36
-6x = 36
X= -6