Question

What phase difference between two otherwise identical traveling waves, moving in the same direction along a stretched string, will result in the combined wave having an amplitude 1.5 times that of the common amplitude of the two combining waves? Express your answer in (a) degrees, (b) radians, and (c) as a fraction of the wavelength.

Answer 1

a) 82.8°

b)1.44 rad

c)0.23λ

Step-by-step explanation:

Wave function form for each wave will be

-> wave 1:

`y_(1)`(x,t)=
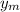`y_{m`sin( kx - ωt)

-> wave 2:

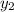`y_{2`(x,t)=
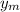`y_{m`sin( kx - ωt +φ)

The summation of above two functions is the resultant wave.

Y(x,t)=
`y_{m`sin( kx - ωt)+
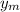`y_{m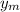`sin( kx - ωt +φ)

Using the trigonometric addition formula for sin i.e

sin(A)+ sin(B) = 2 sin(A+B/2) cos(A-B/2)

Y(x,t)=2
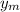`y_{m`cos(φ/2) sin(kx - ωt +φ)

When comparing to the general wave form, the amplitude is 2
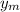`y_{m`cos(φ/2)m

Also,
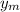`y_{m`cos(φ/2)= 1.5
`y_{m`

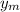
φ/2=
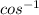`cos^(-1)`(1.5/s)

(a) φ= 82.8°

(b)φ= 82.8π/180 =>1.44 rad

(c) one complete wave is 2π radians

Therefore, for two waves, φ/2π= 1.44/2π => 0.23 fraction of a complete wave from each other i.e they are separated by 0.23λ