Question

When rolling two fair 6 sided dice, what is the probability that the difference between the scores is more than 3?

Answer 1

`1/6`

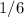
Explanation:

When we say, the difference of scores should be more than 3 it means that the difference can be 4 or 5.

Case 1: The difference of scores is 4.

The possible outcomes can be
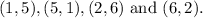`(1,5), (5,1), (2,6) \text{ and }(6,2).` i.e. 4 number of cases are possible.

Case 2: The difference of scores is 5.

The possible outcomes can be
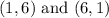`(1,6) \text{ and } (6,1)`. i.e. 2 number of cases.

Here, total number of favorable cases are 4 + 2 = 6.

Total number of cases, when two fair dice are rolled, are 36.

These cases are:

`[(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),\\ (2,1),(2,2),(2,3),(2,4),(2,5),(2,6),\\..\\(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)]}`

Formula:

`\text{Probability of an event = } (Number\ of\ favorable\ cases)/(Total\ number\ of\ cases)`

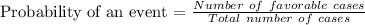
Hence, the probability that the difference of scores is more than 3, at the roll of 2 dice, is
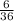`(6)/(36)` i.e.
`(1)/(6)`.

Hence, the required probability is
`(1)/(6)`.