Question

Anna invests $7,000 in an account that compounds interest continuously and earns 7.5%. How long will it take for her

money to reach $105,000? Round to the nearest tenth of a year.
In need of help !!

Answer 1

It will take 36.1 years for her money to reach $105,000.

Explanation:

The amount of money earned after t years in continuous interest is given by:

`P(t) = P(0)e^(rt)`

In which P(0) is the initial investment and r is the interest rate, as a decimal.

Anna invests $7,000 in an account that compounds interest continuously and earns 7.5%.

This means that
`P(0) = 7000, r = 0.075`

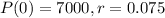
How long will it take for her money to reach $105,000?

This is t for which P(t) = 105000.

`P(t) = P(0)e^(rt)`

`105000 = 7000e^(0.075t)`

`e^(0.075t) = (105000)/(7000)`

`e^(0.075t) = 15`

`\ln{e^(0.075t)} = ln(15)`

`0.075t = ln(15)`

`t = (ln(15))/(0.075)`

`t = 36.1`

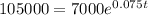
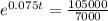
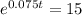
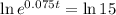
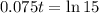
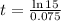
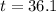
It will take 36.1 years for her money to reach $105,000.