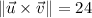Question

Which statement is correct regarding the measurements of the parallelogram?

On a coordinate plane, a parallelogram has points (16, 4), (10, 1), (2, 1), (8, 4).

The base is 6 and the height is 3, so the area is 6 (3) = 18 square units.

The base is 8 and the height is 3, so the area is 8 (3) = 24 square units.

The base is 8 and the height is 4, so the area is 8 (4) = 32 square units.

The base is 8 and the height is 6, so the area is 8 (6) = 48 square units.

Answer 1

B. The base is 8 and the height is 3, so the area is 8 (3) = 24 square units.

Answer 2

The base is 8 and the height is 3, so the area is 8 (3) = 24 square units.

Explanation:

The area of the parallelogram is given by the following expression:

`A = \|\vec u* \vec v\|`

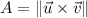
The vectors are, respectively:

`\vec u = (10-2, 1 - 1,0-0)`

`\vec u = (8,0,0)`

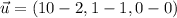
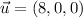
The base of the parallelogram is 8 units.

`\vec v = (8-2, 4-1,0-0)`

`\vec v = (6,3,0)`

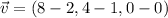
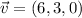
The height of the parallelogram is 3 units.

The cross product of both vectors is:

`\vec u * \vec v = (0,0,24)`

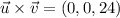
The area of the parallelogram is given by the norm of the resulting vector:

`\|\vec u * \vec v\| = 24`