Answer:
We choose B. (1, 10)
Explanation:
Given the exponential model in the form y = a
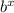
- passes through the points (2, 50)
<=> 50 = a
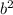
<=> a =
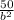 (1)
(1)
- passes through the points (3, 250)
<=> 250 = a
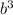 (2)
(2)
Substitute (1) into (2) we have:
250 =
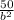
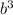
<=> 50b = 250
<=> b = 5
=> a =
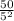 = 2
= 2
Hence, our exponential model is: y =2*
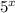
Let analyse all possible answer:
A. (0, 5) we have: y =2*
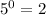 ≠ 5 so it is wrong
≠ 5 so it is wrong
B. (1, 10) we have: y = 2*
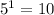 so it is true
so it is true
C. (4, 450) we have: y = 2*
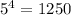 ≠ 450 so it is wrong
≠ 450 so it is wrong
D. (5, 650) we have: y = 2*
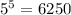 ≠ 650 so it is wrong
≠ 650 so it is wrong
Hence we choose B. (1, 10)