Question

Suppose that the population of the scores of all high school seniors that took the SAT-M (SAT math) test this year follows a normal distribution with unknown population mean and known standard deviation 100. You read a report that says, "On the basis of a simple random sample of 100 high school seniors that took the SAT-M test this year, a confidence interval for population mean is 512.00 ± 25.75." The confidence level for this interval is

Answer 1

`25.75 = z_(\alpha/2) (100)/(√(100))`

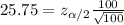
And solving for the critical value we got:

`z_(\alpha/2)= (25.75*10)/(100) = 2.575`

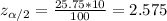
Now we need to find the confidence level and for this case we can use find this probability:

`P(-2.575< Z<2.575)= P(Z<2.575) -P(Z<-2.575)`

And using the normal standard distribution or excel we got:

`P(-2.575< Z<2.575)= P(Z<2.575) -P(Z<-2.575)= 0.9950-0.0050= 0.99`

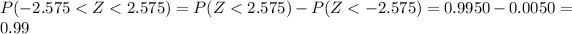
So then the confidence interval for this case is 99%

Explanation:

For this case the random variable X is the scores for the SAT math scores and we know that the distribution for X is normal:

`X\sim N(\mu , \sigma =100)`

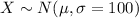
They select a random sample of n =100 and they construc a confidence interval for the true population mean of interest and they got:

`512.00 \pm 25.75`

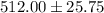
for this problem we need know that the confidence interval for the true mean when the deviation is known is given by:

`\bar X \pm z_(\alpha/2)(\sigma)/(√(n))`

The margin of error is given by:

`ME =z_(\alpha/2) (\sigma)/(√(n))`

And the margin of error for this interval is
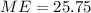`ME = 25.75` then we can solve for the critical value in order to find the confidence level:

`25.75 = z_(\alpha/2) (100)/(√(100))`

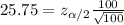
And solving for the critical value we got:

`z_(\alpha/2)= (25.75*10)/(100) = 2.575`

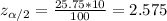
Now we need to find the confidence level and for this case we can use find this probability:

`P(-2.575< Z<2.575)= P(Z<2.575) -P(Z<-2.575)`

And using the normal standard distribution or excel we got:

`P(-2.575< Z<2.575)= P(Z<2.575) -P(Z<-2.575)= 0.9950-0.0050= 0.99`

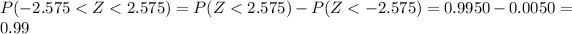
So then the confidence interval for this case is 99%