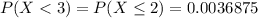Question

Suppose you are taking a 15 question True/False quiz which you are not prepared for. You find yourself simply guessing at every answer. What is the probability that you get less than 3 answers correct?

Answer 1

`P(X=0)=(15C0)(0.5)^0 (1-0.5)^(15-0)=0.0000305`

`P(X=1)=(15C1)(0.5)^1 (1-0.5)^(15-1)=0.000457`

`P(X=2)=(15C1)(0.5)^2 (1-0.5)^(15-2)=0.00320`

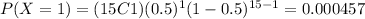
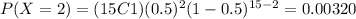
And adding the results we got:

`P(X<3) =P(X \leq 2) = 0.0036875`

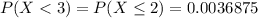
Explanation:

We can define the variable of interest s X representing the number of correct questions for the exam. and we can model this random variable with a binomial distribution. The probability of select the correct answer would be
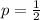`p =(1)/(2)` since is a true/false question.

`X \sim Binom (n =15, p=0.5`

And we want to find this probability:

`P(X <3)= P(X\leq 2)=P(X=0) +P(X=1) +P(X=2)`

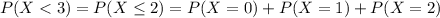
The probability mass function for the Binomial distribution is given as:

`P(X)=(nCx)(p)^x (1-p)^(n-x)`

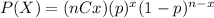
Where (nCx) means combinatory and it's given by this formula:

`nCx=(n!)/((n-x)! x!)`

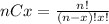
And we want to find this probability:

`P(X \leq 2)=P(X=0)+P(X=1)+P(X=2)`

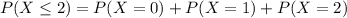
We can find the individual probabilities and we got:

`P(X=0)=(15C0)(0.5)^0 (1-0.5)^(15-0)=0.0000305`

`P(X=1)=(15C1)(0.5)^1 (1-0.5)^(15-1)=0.000457`

`P(X=2)=(15C1)(0.5)^2 (1-0.5)^(15-2)=0.00320`

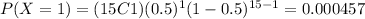
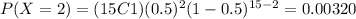
And adding the results we got:

`P(X<3) =P(X \leq 2) = 0.0036875`