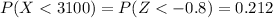Question

Suppose we know that the birth weight of babies is normally distributed with mean 3500g

and standard deviation 500g.

(1) What is the probability that a baby is born that weighs less than 3100g?

a. What are the parameters?

b. Construct the normal distribution density curve, then shade your seeking area.

c. Find the Z-score, and construct the standard normal distribution density curve,

then shade your seeking area.

d. Find the probability.

Answer 1

a)
`\mu = 3500 gr, \sigma = 500g`

`X \sim N(\mu =3500, \sigma =500)`

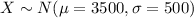
b) For this case we want to find this probability:

`P(X< 3110)`

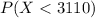
And in the firt figure attached we see the normal standard distirbution with the parameters given and the green area represent the probability that we want to find.

c) For this case the z score is defined as:

`z =(X-\mu)/(\sigma)`

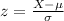
And replacing we got:

`Z= (3100-3500)/(500)= -0.8`

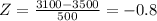
And in the second figure attached we illustrate the probability desired in terms of the z score. With the shaded area representing the probability that z<-0.8

d) We can find this probability using the normal standard distribution or excel and we got:

`P(X<3100) =P(Z<-0.8) = 0.212`

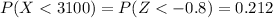
Explanation:

For this problem we define the random variable of interest X defined as "the birth weigth of babies" and the distribution for this variable is normal

Part a

The parameters are given:

`\mu = 3500 gr, \sigma = 500g`

`X \sim N(\mu =3500, \sigma =500)`

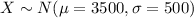
Part b

For this case we want to find this probability:

`P(X< 3110)`

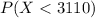
And in the firt figure attached we see the normal standard distirbution with the parameters given and the green area represent the probability that we want to find.

Part c

For this case the z score is defined as:

`z =(X-\mu)/(\sigma)`

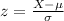
And replacing we got:

`Z= (3100-3500)/(500)= -0.8`

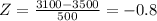
And in the second figure attached we illustrate the probability desired in terms of the z score. With the shaded area representing the probability that z<-0.8

Part d

We can find this probability using the normal standard distribution or excel and we got:

`P(X<3100) =P(Z<-0.8) = 0.212`