Question

Suppose you have a water-balloon launcher. The balloon is 3 ft high when it leaves the launcher. Use the equation 0 = ?16t2 + 38.8t + 3 to find the number of seconds t that the balloon is in the air.

Answer 1

t = 2.5 s

Explanation:

Suppose you have a water-balloon launcher. The balloon is 3 ft high when it leaves the launcher. Its equation is :

`16t^2 + 38.8t + 3 =0`

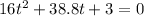
The above equation is a quadratic equation. The general equation is :

`ax^2+bx+c=0`

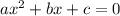
Here, a = 16, b = 38.8 and c = 3

The solution of quadratic equation is given by :

`x=(-b\pm √(b^2-4ac) )/(2a)\\\\t=(-38.8\pm √((38.8)^2-4* (-16)* 3) )/(2* (-16))\\\\t=\frac{-38.8+\sqrt{(38.8)^(2)-4*-16*3}}{-2*16}, \frac{-38.8-\sqrt{(38.8)^(2)-4*-16*3}}{-2*16}\\\\t=-0.075\ s,2.5\ s`

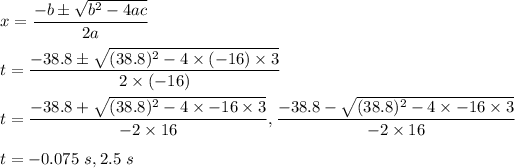
So, at t = 2.5 s the balloon is in air.