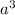Answer:
106.4622
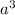
Explanation:
Given the information:
- Leg lengths of
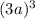 and
and
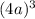
Use the pytagon theory to find the hypotenuse of the triangle
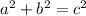
<=>
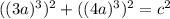
<=>
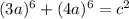
<=>
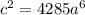
Take the square root of both sides
<=> c = 69.4622
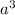
=> expression in simplest form for the perimeter of a right triangle is:
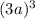 +
+
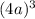 + 69.4622
+ 69.4622
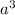
= 27
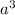 + 64
+ 64
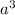 + 69.4622
+ 69.4622
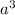
= 106.4622