Question

You are given the sample mean and the population standard deviation. Use this information to construct the​ 90% and​ 95% confidence intervals for the population mean. Which interval is​ wider? If​ convenient, use technology to construct the confidence intervals.

Answer 1

B. is the correct option.

With 90% the population mean price is

in lies in (127.01,134.99). With 95% confidence, it can be said that the population mean price lies in ( 126.24,135.76)

Therefore, the 95% confidence interval is wider than 90%.

The calculation is attached

Answer 2

Question:

You are given the sample mean and the population standard deviation. Use this information to construct the​ 90% and​ 95% confidence intervals for the population mean. Interpret the results and compare the widths of the confidence intervals. If​ convenient, use technology to construct the confidence intervals. A random sample of 45 home theater systems has a mean price of ​$114.00. Assume the population standard deviation is ​$15.30. Construct a​ 90% confidence interval for the population mean.

Answer:

At the 90% confidence level, confidence interval = 110.2484 < μ < 117.7516

At the 95% confidence level, confidence interval = 109.53 < μ < 118.48

The 95% confidence interval is wider

Explanation:

Here, we have

Sample size, n = 45

Sample mean,
`\bar x` = $114.00

Population standard deviation, σ = $15.30

The formula for Confidence Interval, CI is given by the following relation;

`CI=\bar{x}\pm z(\sigma)/(√(n))`

Where, z is found for the 90% confidence level as ±1.645

Plugging in the values, we have;

`CI=114\pm 1.645 * (15.3)/(√(45))`

or CI: 110.2484 < μ < 117.7516

At 95% confidence level, we have our z value given as z = ±1.96

From which we have
`CI=114\pm 1.96 * (15.3)/(√(45))`

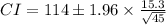
Hence CI: 109.53 < μ < 118.48

To find the wider interval, we subtract their minimum from the maximum as follows;

90% Confidence level: 117.7516 - 110.2484 = 7.5

95% Confidence level: 118.47503 - 109.5297 = 8.94

Therefore, the 95% confidence interval is wider.