Answer:
The spring constant = 104.82 N/m
The angular velocity of the bar when θ = 32° is 1.70 rad/s
Step-by-step explanation:
From the diagram attached below; we use the conservation of energy to determine the spring constant by using to formula:
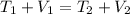
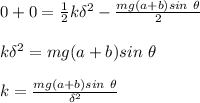
Also;
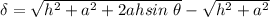
Thus;

where;
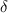 = deflection in the spring
= deflection in the spring
k = spring constant
b = remaining length in the rod
m = mass of the slender bar
g = acceleration due to gravity
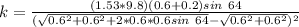
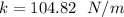
Thus; the spring constant = 104.82 N/m
b
The angular velocity can be calculated by also using the conservation of energy;
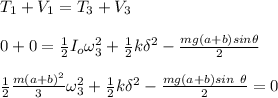
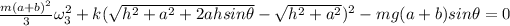
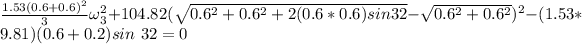
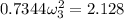

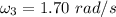
Thus, the angular velocity of the bar when θ = 32° is 1.70 rad/s