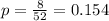Question

You are dealt one card from a standard​ 52-card deck. Find the probability of being dealt a card greater than 2 and less than 5. The probability of being dealt a card greater than 2 and less than 5 is........

Answer 1

`p =(Possible cases)/(Total cases)`

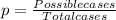
And replacing 8 for the possible cases and 52 for the total number of cards for a single selection we got:

`p =(8)/(52)= 0.154`

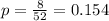
Explanation:

For a standard deck we need to remember that we have 4 types suits of Spades, Hearts, Diamonds, and Clubs. And in total 13 possible options A,2,3,4,5,6,7,8,9,10,J,Q,K.

If we want the probability that a card selected would be greater than 2 and less than 5 means that we are interested in the cards with denomination 3's and 4's because the card can't be 2 or 5.

And from the previous info we know that we have four cards for the 4's and four for the 3's so then we have a total of 8 possible cards in the standard deck of 52 who satisfy the conditions required.

And then we can find the probability desired with this formula:

`p =(Possible cases)/(Total cases)`

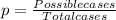
And replacing 8 for the possible cases and 52 for the total number of cards for a single selection we got:

`p =(8)/(52)= 0.154`