Question

The energy of any one-electron species in its nth state (n = principal quantum number) is given by E = –BZ2 /n2 where Z is the charge on the nucleus and B is 18 2.180 10  J. a) Find the ionization energy of the Be3+ ion in its first excited state in kilojoules per mole. b) Find the wavelength of light given off from the Be3+ ion by electrons dropping from the fourth (n = 4) to the second (n = 2) energy levels.

Answer 1

Step-by-step explanation:

(a) The given data is as follows.

B =
`2.180 * 10^(-18) J`

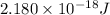
Z = 4 for Be

Now, for the first excited state
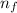`n_(f)` = 2; and
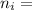`n_(i) = \infinity` if it is ionized.

Therefore, ionization energy will be calculated as follows.

I.E =
`(-Bz^(2))/(\infinity^(2)) - ((-2.180 * 10^(-18) J /times (4)^(2))/((2)^(2)))`

=
`8.72 * 10^(-18) J`

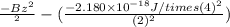
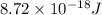
Converting this energy into kJ/mol as follows.

`8.72 * 10^(-18) J * 6.02 * 10^(23) mol`

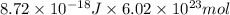
= 5249 kJ/mol

Therefore, the ionization energy of the
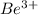`Be^(3+)` ion in its first excited state in kilojoules per mole is 5249 kJ/mol.

(b) Change in ionization energy is as follows.

`\Delta E = -Bz^(2)((1)/((4)^(2)) - {1}{(2)^(2)}) = (hc)/(\lambda)`

`(hc)/(\lambda) = 0.1875 * 2.180 * 10^(-18) J * (4)^(2)`

`\lambda = (6.626 * 10^(-34) * 2.998 * 10^(8) m/s)/(0.1875 * 2.180 * 10^(-18) J * 16)`

=
`303.7 * 10^(-10) m`

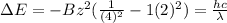
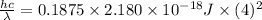
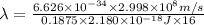
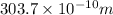
or, =
`303.7^(o)A`

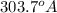
Therefore, wavelength of light given off from the
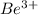`Be^(3+)` ion by electrons dropping from the fourth (n = 4) to the second (n = 2) energy levels
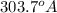`303.7^(o)A`.