Answer:
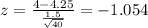
And we can find the following probability:
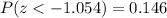
And the last probability can be founded using the normal standard distribution or excel.
Explanation:
For this case we define the random variable X as the ages of vehicles. We know the following info for this variable:
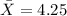 represent the mean
represent the mean
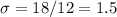 represent the deviation in years
represent the deviation in years
They select a sample size of n=40>30. And they want to find this probability:
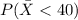
Since the sample size is large enough we can use the central limit theorem and the distribution for the sample mean would be:

We can use the z score formula given by:
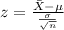
And if we find the z score for 4 we got:
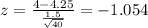
And we can find the following probability:
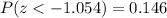
And the last probability can be founded using the normal standard distribution or excel.