Answer:
The letters of the word LUMBERJACKS can be arranged in 39,916,800 unique ways.
The letters of the word HIGHLIGHT can be arranged in 15,120 unique ways.
The letters of the word COOKBOOK can be rearranged in 840 unique ways.
88! divided by 86! is (88*87*86!)/(86!) = 7656
Explanation:
A word has n letters.
The are m repeating letters, each of them repeating
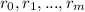 times
times
So the number of distincts ways the letters can be arranged is:
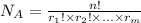
LUMBERJACKS:
11 letters, none repeating. So
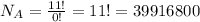
The letters of the word LUMBERJACKS can be arranged in 39,916,800 unique ways.
HIGHLIGHT
9 letters
H repeats 3 times
G repeats 2 times
I repeats 2 times
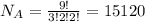
The letters of the word HIGHLIGHT can be arranged in 15,120 unique ways.
COOKBOOK:
8 letters
O repeats 4 times
K repeats 2 times
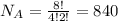
The letters of the word COOKBOOK can be rearranged in 840 unique ways.
What is 88! divided by 86! ?
The factiorial of a number n can be writen as

Then
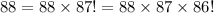
Then
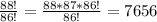
88! divided by 86! is (88*87*86!)/(86!) = 7656