Answer:
N = 16 measurements
Explanation:
A method produces a random error for each measurement of 4%
A percent error of equal to or less than 1% is required.
We want to find out the minimum number of measurements that must be collected.
The standard error is given by
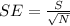
Where s is the standard deviation and N is the number of measurements.
We are given standard deviation equal to 4% and SE equal to 1%
So re-arranging the above equation for N
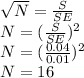
Therefore, a minimum 16 number of measurements are needed.