Question

The mean of hours that the average person watches television each day is 4.18 hours with a standard deviation of 1.19 hours. Find probability that someone watches between 3 and 5 hours a day

Answer 1

`z = (3-4.18)/(1.19)=-0.992`

`z = (5-4.18)/(1.19)=0.689`

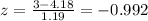
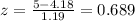
And we can find this probability with this difference:

`P(-0.992<z<0.689) = P(z<0.689) -P(z<-0.992) =0.752 -0.161=0.591`

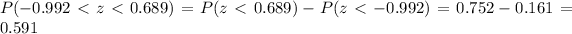
And then we can conclude that the probability that someone watches between 3 and 5 hours a day is approximately 0.591 using a normal distribution

Step-by-step explanation:

For this case we can define the random variable X as "hours that a person watches television". For this case we don't have the distribution for X but we have the following parameters:

`\mu = 4.18,\sigma =1.19`

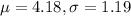
We can assume that the distribution for X is normal

`X \sim N(\mu = 4.18 , \sigma =1.19)`

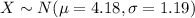
And we want to find this probability:

`P(3 <X<5)`

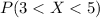
And we can use the z score formula given by:

`z=\frac[X- \mu}{\sigma}`

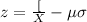
And we can find the z score for each limit and we got:

`z = (3-4.18)/(1.19)=-0.992`

`z = (5-4.18)/(1.19)=0.689`

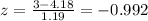
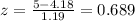
And we can find this probability with this difference:

`P(-0.992<z<0.689) = P(z<0.689) -P(z<-0.992) =0.752 -0.161=0.591`

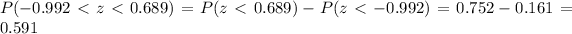
And then we can conclude that the probability that someone watches between 3 and 5 hours a day is approximately 0.591 using a normal distribution