Question

(Sec. 8.4) In a sample of 165 students at an Australian university that introduced the use of plagiarism-detection software in a number of courses, 55 students indicated a belief that such software unfairly targets students. Does this suggest that a majority of students at the university do not believe that it unfairly targets them? Test the appropriate hypotheses at the 5% significance level.

Answer 1

`z=\frac{0.667 -0.5}{\sqrt{(0.5(1-0.5))/(165)}}=4.29`

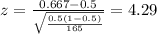
The p value for this case is given by:

`p_v =P(z>4.29)=8.93x10^(-6)`

Since the p value is lower than the significance level we have enough evidence to conclude that the true proportion is significantly higher than 0.5 at 5% of significance.

Explanation:

Information given

n=165 represent the random sample selected

55 represent the students indicated a belief that such software unfairly targets students

X =165-55= 110 represent students who NOT belief that such software unfairly targets students

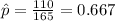`\hat p=(110)/(165)=0.667` estimated proportion of students who NOT belief that such software unfairly targets students

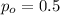`p_o=0.5` is the value that we want to check

`\alpha=0.05` represent the significance level

z would represent the statistic

`p_v` represent the p value

System of hypothesis

We want to check if the majority of students at the university do not believe that it unfairly targets them, and the system of hypothesis are:

Null hypothesis:
`p\leq 0.5`

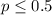
Alternative hypothesis:
`p > 0.5`

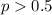
The statistic for this case is given by:

`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

After replace we got:

`z=\frac{0.667 -0.5}{\sqrt{(0.5(1-0.5))/(165)}}=4.29`

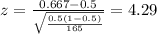
The p value for this case is given by:

`p_v =P(z>4.29)=8.93x10^(-6)`

Since the p value is lower than the significance level we have enough evidence to conclude that the true proportion is significantly higher than 0.5 at 5% of significance.