Question

) You want to rent an unfurnished one-bedroom apartment after you graduate from high school. The mean monthly rent for a random sample of 10 apartments advertised in the local newspaper is $940. The margin of error for a 95% confidence interval is $160. Find the 95% confidence interval for the mean monthly rent for unfurnished one-bedroom apartments available for rent in this community. Write your answer in this format: x to y

Answer 1

`940-160=780`

`940+160=1100`

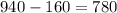
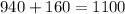
So then we are 95% confident that the true mean for the monthly rent is between 780 and 1100

Explanation:

For this case we can define the following random variable X as the monthly rent and we know the following properties given:

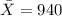`\bar X= 940` represent the sample mean

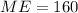`ME = 160` represent the margin of error

n = 10 represent the sample size

The confidence interval for the true mean is given by:

`\bar X \pm z_(\alpha/2) \sqrt{(\sigma)/(√(n))}`

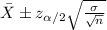
And is equivalent to:

`\bar X \pm ME`

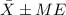
And for this case if we replace the info given we got:

`940-160=780`

`940+160=1100`

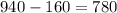
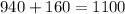
So then we are 95% confident that the true mean for the monthly rent is between 780 and 1100

Answer 2

$780 to $1100

Explanation:

A confidence interval has two bounds. A lower bound and an upper bound. They are dependent of the sample mean and of the margin of error M.

In this problem:

Sample mean: $940

Margin of error: $160

The lower end of the interval is the sample mean subtracted by M. So it is 940 - 160 = $780

The upper end of the interval is the sample mean added to M. So it is 940 + 160 = $1100

So the answer is

$780 to $1100