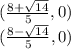Y-INTERCEPT
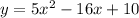
The y-intercept is where the equation/curve/parabola cosses the y-axis.
The y-axis is where x = 0. (The x-axis is where y = 0)
To find the y-intercept:
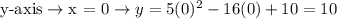
The y-intercept must be at (0, 10)
X-INTERCEPT (ROOTS/SOLUTIONS)

We need to use the quadratic formula
The quadratic formula helps us find what values of
 make the equation = 0
make the equation = 0
Quadratic formula:

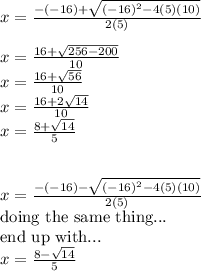
The x-intercepts are at: