Question

The rate constant of the elementary reaction C2H5CN(g) → CH2CHCN(g) + H2(g) is k = 7.21×10-3 s-1 at 634 °C, and the reaction has an activation energy of 247 kJ/mol. (a) Compute the rate constant of the reaction at a temperature of 741 °C. _________ s-1 (b) At a temperature of 634 °C, 96.1 s is required for half of the C2H5CN originally present to be consume. How long will it take to consume half of the reactant if an identical experiment is performed at 741 °C? (Enter numbers as numbers, no units. For example, 300 minutes would be 300. For letters, enter A, B, or C. Enter numbers in scientific notation using e# format. For example 1.43×10-4 would be 1.43e-4.)

Answer 1

the rate constant of the reaction at a temperature of 741 °C is
`0.22858 \ s^(-1)`

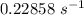
it will take 3.0313 s to consume half of the reactant if an identical experiment is performed at 741 °C

Step-by-step explanation:

Given that :

`k_1 = 7.21*10^(-3) s^(-1) \\ \\ E_a = 247 kJ/mol \ \ \ = 247*10^3 \ J/mol \\ \\ T_1 = 634 ^ {^0} C= (273 + 634) K = 907 \ K \\ \\ T_2 = 741^(^0 ) C = (273+ 741) K = 1014 \ K \\ \\ R =8.314 \ \ J/mol/K`

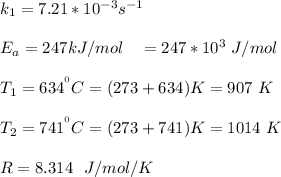
a)

According to Arrhenius Equation ;

`In(k_2)/(k_1) = -(Ea)/(R)((1)/(T_2) -(1)/(T_1) )`

`In(k_2)/(7.21*10^(-3)) = -(247*10^3)/(8.314)((1)/(1014) -(1)/(907) )`

`In(k_2)/(7.21*10^(-3)) = -(247*10^3)/(8.314)((907-1014)/(907*1014) )`

`In(k_2)/(7.21*10^(-3)) = (-247*10^3*-107)/(8.314*907*1014)`

`In(k_2)/(7.21*10^(-3)) = 3.456412`

`(k_2)/(7.21*10^(-3)) =e^{ 3.456412`

`k_2 = 31.70302 * 7.21*10^(-3)`

`k_2 = 0.22858 \ s^(-1)`

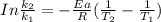
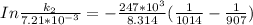
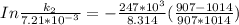
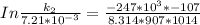
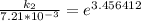
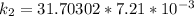
Therefore , the rate constant of the reaction at a temperature of 741 °C is
`0.22858 \ s^(-1)`

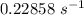
b) Given that :

`t_((1/2)) = 96.1 \ s`

`k_1 = (0.693)/( t_((1/2)))`

`k_1 = (0.693)/( 96.1 \ s)`

`k_1 = 7.211*10^(-3) \ s^(-1)`

`In(k_2)/(7.211*10^(-3)) = -(247*10^3)/(8.314)((1)/(1014) -(1)/(907) )`

`In(k_2)/(7.211*10^(-3)) = -(247*10^3)/(8.314)((907-1014)/(907*1014) )`

`In(k_2)/(7.211*10^(-3)) = (-247*10^3*-107)/(8.314*907*1014)`

`In(k_2)/(7.211*10^(-3)) = 3.456412`

`(k_2)/(7.211*10^(-3)) =e^{ 3.456412`

`k_2 =e^{ 3.456412 * 7.21*10^(-3)`

`k_2 = 0.22862 \ s^(-1)`

`t_((1/2)_2)} = (0.693)/(k_2)`

`t_((1/2)_2)} = (0.693)/(0.22862)`

`t_((1/2)_2)} =3.0313 \ s`

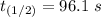
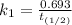
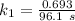
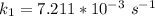
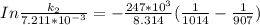
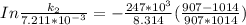
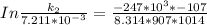
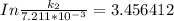
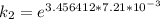
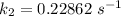
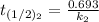
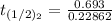
it will take 3.0313 s to consume half of the reactant if an identical experiment is performed at 741 °C