The sum of the first 6 66 terms of a geometric series is 15 , 624 15,62415, comma, 624 and the common ratio is 5 55. What is the first term of the series?

Question

asked Apr 17, 2021 85.5k views

1 Answer

Tony Arnold · Answer 1 · 2021-04-20T20:29:01+0000

Answer:

The first term of the series is 4

Explanation:

The sum of the first 6 terms of a geometric series is 15 , 624 and the common ratio is 5 .

To find the first term, we use the formula for the sum of terms in a geometric series.

Since the common ratio of the series is greater than 1, the sum of
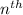n^(th) term of the geometric series is;

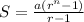
S = (a(r^n - 1))/(r - 1)

where r = common ratio

a = first term

When S = 15,624, r = 5 and n = 6, the first term, a, will be:

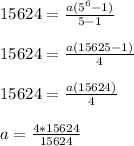
$15624 = (a(5^6 - 1))/(5 - 1) \\\\15624 = (a(15625 - 1))/(4)\\\\15624 = (a(15624))/(4)\\\\a = (4 * 15624)/(15624)$

a = 4

The first term of the series is 4.